
|
|
図-1(a)
物質、エネルギー、運動量の保存、移動、生成逸散条件 [1] |
|
|
図-1(b)
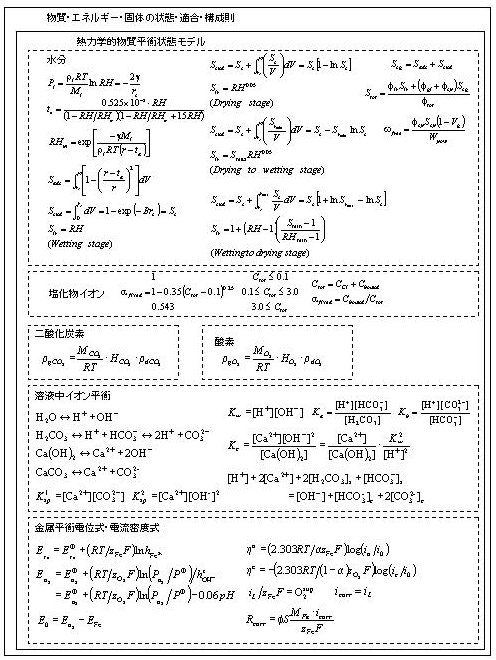
物質・エネルギー・固体の状態/適合構成則 (No.1) [1] |

|
|
図-1(c)
物質・エネルギー・固体の状態/適合構成則 (No.2) [1] |
2 構造力学解析と材料物理化学解析の結合
構造力学では、釣り合い条件、変形適合条件、材料構成式を連立して解くことで、応答結果を得る。この規範は、過去100年、不変である。材料特性や品質の変遷を解く場合には、質量とエネルギーの保存則、平衡/非平衡状態則、状態変化の速度則を連立して解く。釣り合い式は運動量保存則で等価に表現することができるので、構造力学体系と材料物理化学系は、例えば図-1のように数理統合することが可能である[1]。運動量(構造力学指標)、エンタルピー(熱エネルギー)、水分(水蒸気と液体凝縮水)、酸素(溶存および気体)、二酸化炭素(溶存および気体)、塩化物イオンを連携システムの自由度(解析上の変数)とすれば、対応する物理化学事象として、材料変形、物質・エネルギー移動、水和反応、材料形成・劣化、炭酸化反応、酸化腐食反応を熱力学第一法則(質量・エネルギーの保存)と第二法則(相互平衡条件)の基に記述することで、システムは数学的にも完備(complete)となる。図-1の支配方程式は何れも非線形である。たとえば構造力学系では、応力がひずみに対して非線形であると同時に、温度、水和度、水分状態などの物性系の自由度(温度、間隙水圧、酸素濃度、二酸化炭素濃度、塩化物イオン濃度)の非線形な関数にもなっている。これらを満たす非線形解を得る技術について、言及してみたい。
前段階として、図-1の支配方程式を場所と時間で離散化する必要がある。これには、古典的な重み付き残差法が、非線形問題一般に対して有効である。最終的には、図-1(a)の保存則を離散化した方程式に集約されるのであるが、これらを一括してマトリックス法で解く方法が考えられる。x-y-zの節点変位、温度、細孔中の凝縮水圧力、塩化物イオン濃度、酸素濃度、二酸化炭素濃度の8自由度の上に、1つの有限要素(20節点)に対して160×160の全体感度マトリックスと160元の等価ベクトル(節点力、熱流束、水分・塩分・酸素・二酸化炭素流束)が生成される。最終的に要素毎の等価ベクトルを足し合わせ、全体でゼロベクトルとなる節点自由度を求めることに帰着する。マトリックス構造力学と同じ解法が適用できる。

|
|
図-1(a)
物質、エネルギー、運動量の保存、移動、生成逸散条件 [1] |

|
|
図-1(b)
物質・エネルギー・固体の状態/適合構成則 (No.1) [1] |

|
|
図-1(c)
物質・エネルギー・固体の状態/適合構成則 (No.2) [1] |
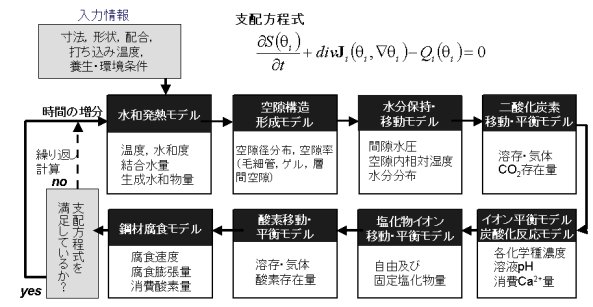
上記は非線形解析技術の定石であるが、このプロジェクトのスタート(1990年)から4年目にして、この方法を放棄せざるを得ない状況に至った。全体行列を組むと、対角項に現れる数値が、最大で20桁も異なったからである。現在は、超大規模計算や並列ベクトル計算で使用されるような、分散-整合型のアルゴリズムを、非線形解析法として採用している(図-2)。直列に質量・エネルギー保存則を解きながら、複数の系にまたがる物理化学量を共通領域に書き込んでは更新していく(図-2(a))[1][2]。あるいは、個々の保存則を個別のCPUで解きながら、高速バスで相互にデータを共有(参照と更新)しつつ、同期(材齢)をとりながら並列演算を進める、という方法である(図-2(b))[1][3]。
全体行列の対角項に大きな桁違いが発生するのは、そもそも異なる物理化学現象を一つの全体行列に畳み込んだこと、そしてナノ、マイクロスケールの現象とメートルスケールの挙動とを同時に、しかも非零非対角項の存在のもとに、システムを一気に解こうとするからである(図-3,4)。
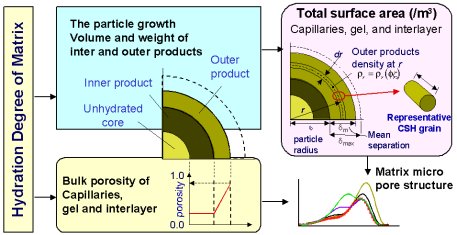
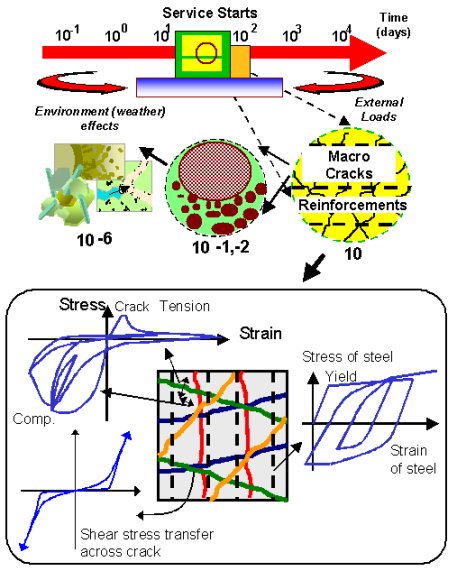
たとえば、構造体中のセメントコンクリートの水和反応速度は,水和反応で形成されるセメント硬化体の幾何構造にも影響を受ける(特に低水セメント比コンクリートの場合)[2][4]。生成されたCSHゲルの層間空隙にすでに挟み込まれた水分子と,ゲル表面に強固に吸着される水分子(ナノスケール)は水和反応に寄与せず、マイクロスケールの細孔構造に凝縮する水が、水和反応に寄与するからである(図3)[2][4]。さらに、これらの水は空隙中の水蒸気分圧に依存(平衡)し、同時に水の移動に影響を及ぼす[2]。これによって細孔中の間隙水圧力は変動し、セメント硬化体に体積変化をもたらし、コンクリート構造の変形・たわみ(メートルスケール)と、ひび割れ損傷や応力変化があらわれる[1][3]。そしてひび割れ損傷は水やその他の物質移動を促進させ、結果として鋼材酸化腐食、炭酸化反応に影響を及ぼし、細孔組織構造の変化をもたらす[1][3]。ゲル空隙中の吸着層(水分子のおよそ10倍程度)とコンクリート部材のたわみは、以上の例のように連携しており、「風が吹けば桶屋が儲かる」式の複雑な相互依存が、ナノからメートルスケールまで広がる(図4)。したがって,最終的には統合した全体感度マトリックスの非対角項に、数値として現れるのである。
このシステムを一気に解こうとすれば、桁落ちは倍精度演算でも確実に発生する。従属変数を固定した状態で各物理現象をひとまず解き、共通変数が変更された段階で再度解き直し、全体系が収束するまで繰り返す,分散-整合型解法が図2(a)である。
所定の精度を確保するには、適切な時間差分を採る必要がある。例えば、水和反応は材齢数時間から数日が活発に進行する事から、温度に関する解析の時間差分はある程度、小さく設定しなければならないが、1ヵ月以降は日単位の時間差分で必要十分となる場合が多い[2][4]。一方、炭酸化反応を追跡する場合には、暴露した直後で15秒〜30秒単位の時間差分が必要となる。部材表面の極近傍で、細孔内の凝縮水中の溶解イオン(カルシウム、炭酸、炭酸水素、水酸基、プロトン)濃度が,急激に変化するからである[1][5]。図-2(a)の分散型で解く場合、各々の現象で適切な時間差分を別個に設定でき、システムで共有する情報は、最も時間差分の長い系に合わせて更新するといった,柔軟な対応が可能となる。もし、全系を統括して一挙に離散方程式を解くとすれば、最も小さい時間差分に全体を合わせなければならない。
以上の経緯から、コンクリート工学に関する非線形解析技術の進展は、分散-整合型に向かうのが適当ではないかと著者らは考えている。この方法によれば、すでに保有している複数の解析プログラムを、マルチタスク処理が可能なOS上(現在では、全てのPC、EWSで可能)で簡単に統合することができる。図2(b)のシステムによれば,異なる言語で書かれたアルゴリズムでも、共通データ領域をシステム内に設けることで、相互にデータを授受共有しながら計算を進めることができる。拡張性に優れている点も重要である。現在、 CSHゲルの溶解とカルシウムイオン移動、ならびに電場磁場をシステムに追加しているが、フレームを拡張するためのコード作成作業に要した時間は、1日程度で済んでいる。
|
|
図-2(a).
質量・エネルギーの保存条件と連立解法[1][2] |

|
|
図-2(b).
構造系と材料物理化学系との連成解の求め方[1][3] |
|
|
図-3.
ナノ-マイクロスケールの構造モデル化[2][4] |
|
|
図-4.
メートルスケールのモデル化と微視スケールのモデル化
[1][2][6][7] |
| 目次に戻る | 次へ |